To open the Symbol Property dialog box, you can either select the Object Select icon from the Layout Tab, or if you have a symbol selected you can hover over the dynamic and single click it.

The layout tab responsible for your score layout.

Symbol Velocity

Although a symbol has a predefined velocity, you may wish to edit this velocity, from 0 – 127.

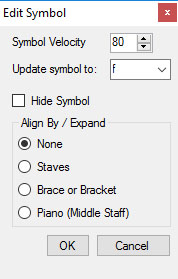
The property dialog box for a velocity symbol.

Update Symbol

If you want to update a velocity symbol from f to p, you can do so here.

Hide Symbol

You can hide a symbol if you want an effect, but don’t want to display the symbol on the score.  The shortcut for hiding a symbol is to hover over the symbol, and press H.

Align By / Expand

If a velocity symbol has already been placed on the score and you decide that you want to expand that symbol and/or align it, just double click on the symbol and a properties dialog box will open.

You can expand and/or align the symbol by choosing Staves, Brace or Bracket, or Piano (Middle Staff).